Inference-Time Scaling for Diffusion Models beyond Scaling Denoising Steps

Innate Inference-Time Scaling of Diffusion

In recent years a family of flexible generative model based on transforming pure noise $\varepsilon \sim \mathcal{N}(0, \mathbf{I})$ into data $x_* \sim p(x)$ has emerged. This transformation can be described by a simple time-dependent process $$x_t = \alpha_t x_* + \sigma_t \varepsilon$$ with t defined on $[0, T]$, $\alpha_t, \sigma_t$ being time-dependent functions and chosen such that $x_0 \sim p(x)$, $x_T \sim \mathcal{N}(0, \mathbf{I})$. At each $t$, $x_t$ has a conditional density $p_t(x | x_*) = \mathcal{N}(\alpha_t x_*, \sigma_t^2\mathbf{I})$, and our goal is to estimate the marginal density $p_t(x) = \int p_t(x | x_*) p(x) \mathrm{d}x$. Diffusion-Based and Flow-Based Models simulate a vector field via an ordinary differential equation (ODE) or a stochastic differential equation (SDE) to estimate the marginal density $p_t(x)$ and perform sampling.

These generation processes usually starts from pure noise and requires multiple forward passes of trained models to denoise and obtain clean data. These forward passes are thus dubbed denoising steps. Since the number of denoising steps can be adjusted to trade sample quality for computational cost, the generation process of diffusion models naturally provides flexibility in allocating inference-time computation budget. Under the context of generative models, such computation budget is also commonly measured by the number of function evaluations (NFE), to ensure a reasonable comparison with other families of models that use iterative sampling processes but without denoising capabilities. Empirical observations have indicated that by investing compute into denoising steps alone, performance gains tend to plateau after a certain NFEs, limiting the benefits of scaling up computation during inference. Therefore, a new framework needs to be designed.

In theory, there is explicit randomness in the sampling of diffusion models: the randomly drawn initial noise, and the optional subsequent noise injected via procedures like SDE and Restart Sampling Nonetheless, because the model evaluations are inherently deterministic, there is a fixed mapping from these noises to the final samples. It has been shown that some noises are better than others, suggesting that it is possible to push the inference time scaling limit by devoting more compute to finding the more preferable noises for sampling.

Inference-Time Scaling as Search Problems

We frame the inference-time scaling as a search problem over the sampling noises; in particular, how do we know which sampling noises are good, and how do we search them?

On a high-level, there are two design axes we propose to consider:

• Verifiers: pre-traied models that are capable of providing feebacks on the quality of the noise candidates; concretely, they takes in the generated samples and optionally the corresponding conditions, and outputs a scalar value as the score for each generated sample.
• Algorithms: functions that are used to find better noise candidates based on the feedbacks from the verifiers. Formally defined, algorithms are functions $$f: \mathcal{V} \times D_\theta \times \{\mathbb{R}^{H \times W \times C} \times \mathbb{R}^d\}^N \to \mathbb{R}^{H\times W \times C}$$ that takes in a verifier $\mathcal{V}$, a pre-trained Diffusion Model $D_\theta$, and $N$ pairs of generated samples and corresponding conditions, and outputs the best initial noises according to the deterministic mapping between noises and samples. Throughout this search procedure, $f$ typically performs multiple forward passes through $D_\theta$. We refer to these additional forward passes as the search cost, which we measure in terms of NFEs as well.

Verifiers

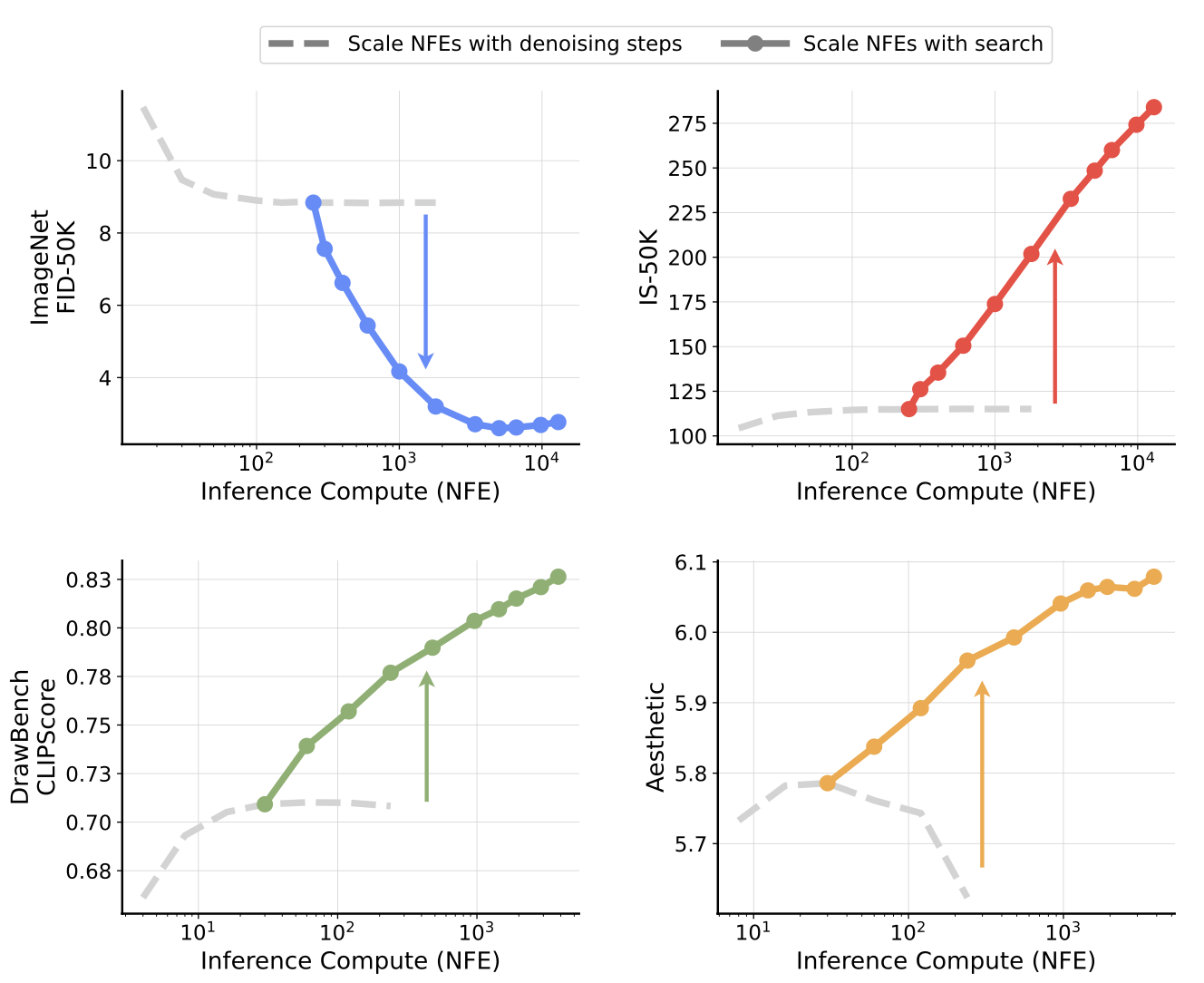
Oracle Verifier, which utilizes full privileged information about the final evaluation of the selected samples. On ImageNet, we directly take the most commonly-used FID and IS as the oracle verifiers. For IS, we select the samples with highest classification probability output by a pretrained InceptionV3 model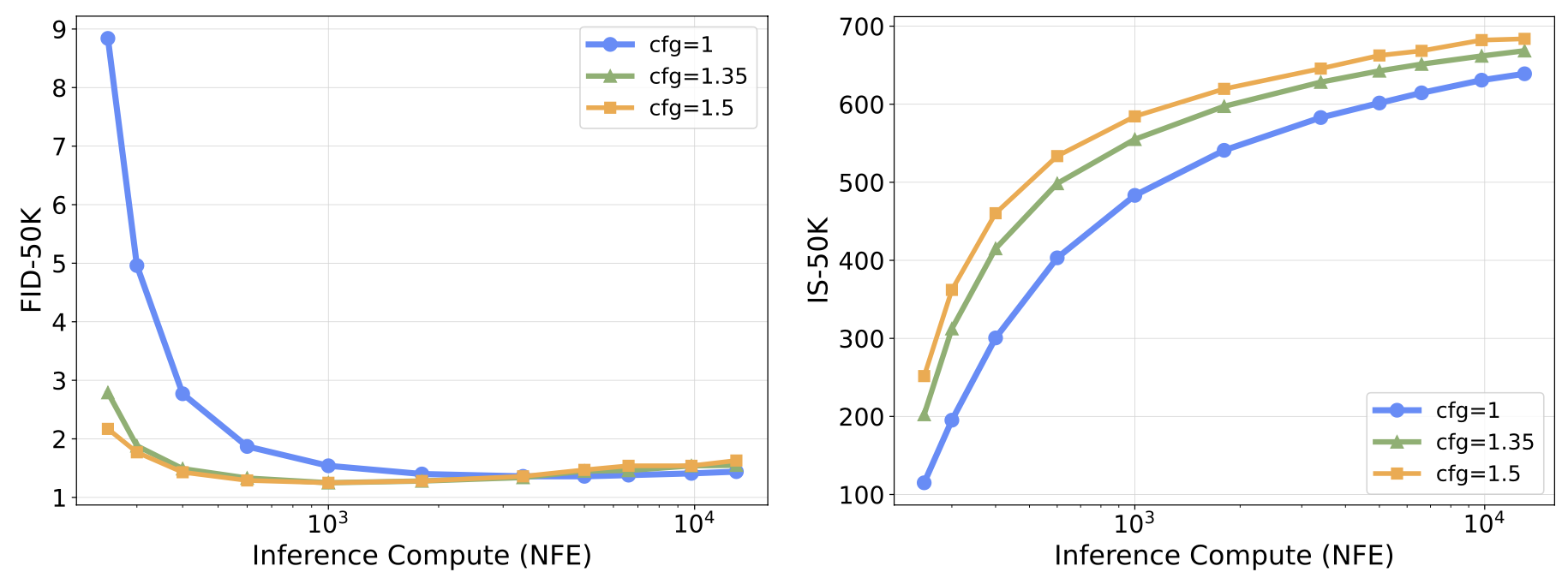 of the conditioning class. For FID, we use the pre-calculated ImageNet Inception feature statistics as reference, and we greedily choose the sample that minimizes the divergence against the ground-truth statistics.

Supervised Verifier, which has access to pre-trained models for evaluating both the quality of the samples and their alignment with the specified conditioning inputs. This is a more realistic setup as the pre-trained models are not directly linked to the final evaluation of the samples, and we want to investigate if the supervised verifiers can still provide reasonable feedbacks and enable effective inference-time scaling.

Although this strategy effectively improves the IS of the samples comparing to purely scaling NFEs with increased denoising steps, the classifiers we use are only partially aligned with the goal of FID score, since they operate point-wise and do not consider the global statistics of the samples. This can lead to a significant reduction in sample variance and eventually manifests as mode collapse as the compute increases, as demonstrated below by the increasing Precision and the decreasing Recall.

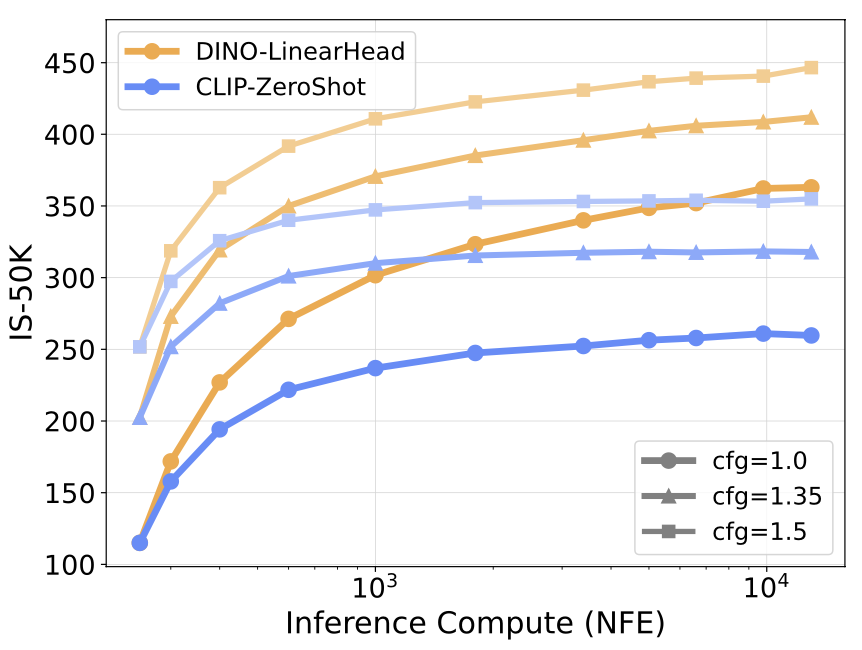
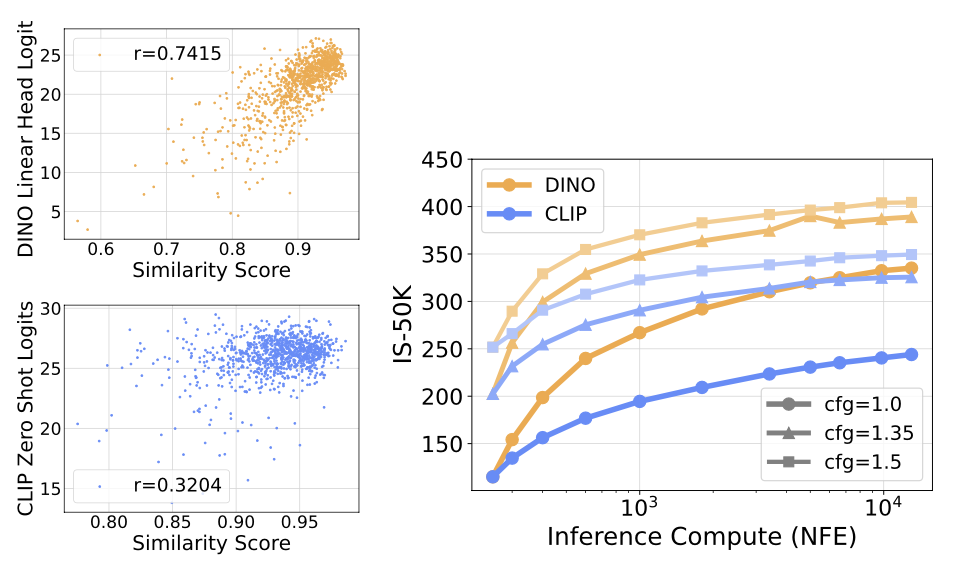
Self-Supervised Verifier, which uses the feature space (extracted by DINO / CLIP, respectively) cosine similarity of samples at low noise level ($\sigma = 0.4$) and clean samples ($\sigma = 0.0$) to evaluate the quality of initial noises. We found that such similarity score is highly correlated with the logits output by the DINO / CLIP classifiers, and thus use it as an effective surrogate for the supervised verifier, as demonstrated below.

Algorithms

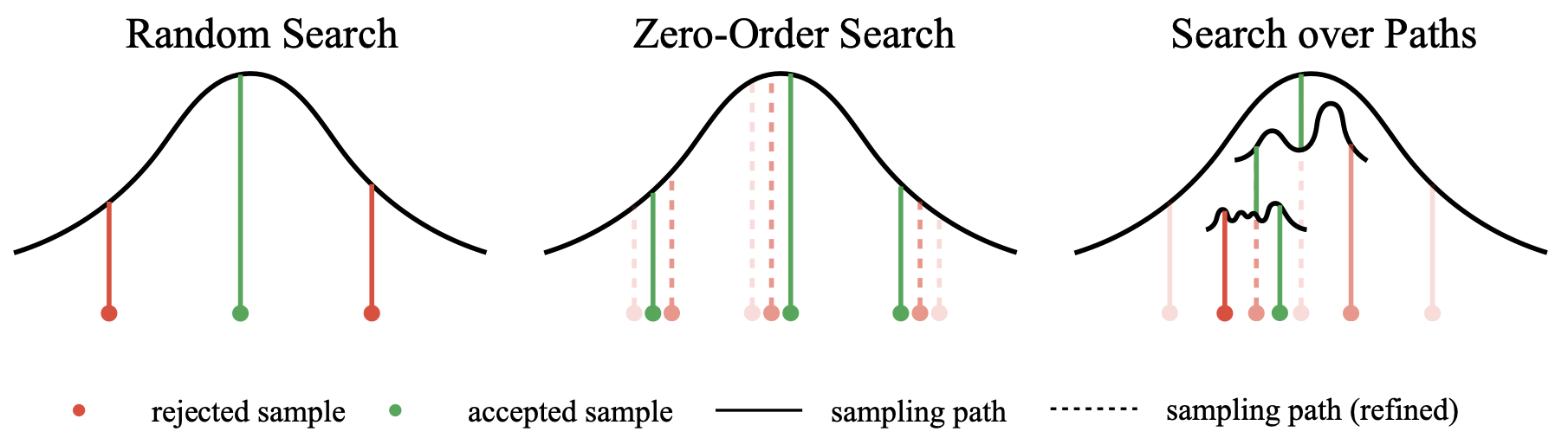
Random Search, which is essentially a Best-of-N strategy applied once on all noise candidates, and the primary axis for scaling NFEs in search is simply the number of noise candidates to select from. Its effectiveness has been demonstrated in previous section, and we note that since its search space is unconstrained, it accelerates the converging of search towards the bias of verifiers, leading to the loss in diversity. Such phenomenon is similar to reward hacking in reinforcement learning, and thus we term it as Verifier Hacking.

Zero-Order Search, which is similar to Zero-Order Optimization, and we specified the detailed procedure below.

1. we start with a random Gaussian noise $\mathbf{n}$ as pivot.
2. find $N$ candidates in the pivot's neighborhood. Formally, the neighborhood is defined as $S_{\mathbf{n}}^\lambda = \{\mathbf{y}: d(\mathbf{y}, \mathbf{n}) = \lambda\}$, where $d(\cdot, \cdot)$ is some distance metric.
3. run candidates through an ODE solver to obtain samples and their corresponding verifier scores.
4. find the best candidates, update it to be the pivot, and repeat steps 1-3.

Search over Paths, which iteratively refine the diffusion trajectory, and we specified the detailed procedure below.

1. sample $N$ initial i.i.d. noises and run the ODE solver until some noise level $\sigma$. The noisy samples $\mathbf{x}_\sigma$ serve as the search starting point.
2. sample $M$ i.i.d noises for each noisy samples, and simulate the forward noising process from $\sigma$ to $\sigma + \Delta f$ to produce $\{\mathbf{x}_{\sigma + \Delta f}\}$ with size $M$.
3. run ODE solver on each $\mathbf{x}_{\sigma + \Delta f}$ to noise level $\sigma + \Delta f - \Delta b$, and obtain $\mathbf{x}_{\sigma + \Delta f - \Delta b}$. Run verifiers on these samples and keep the top $N$ candidates. Repeat steps 2-3 until the ODE solver reaches $\sigma = 0$
4. run the remaining $N$ samples through random search and keep the best one.

Inference-Time Scaling in Text-to-Image

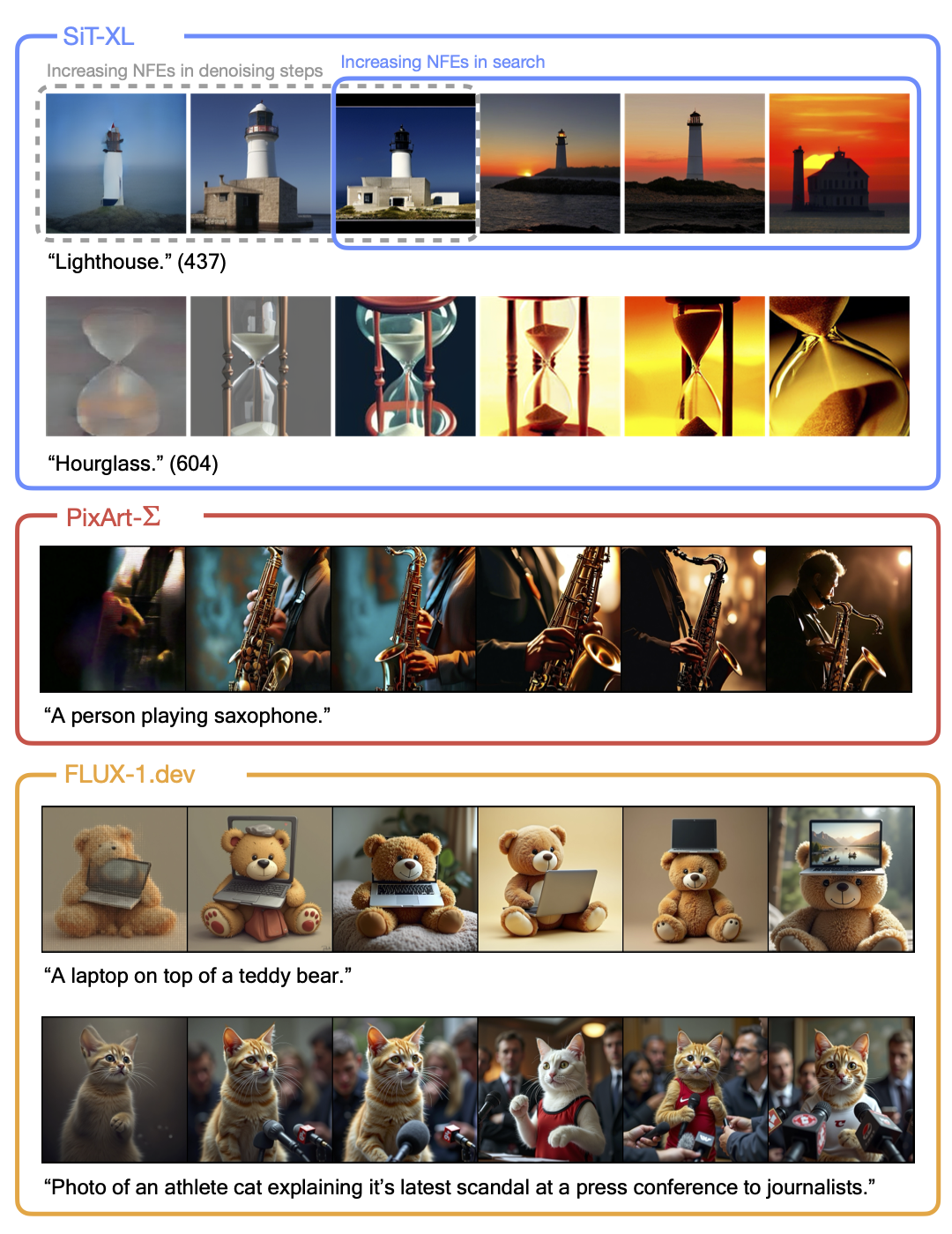
With the instantiation of our search framework, we proceed to examine its inference-time scaling capability in larger-scale text-conditioned generation tasks, and study the alignment between verifiers and specific image generation tasks.

Datasets. For a more holistic evaluation of our framework, we use two datasets: DrawBench and T2I-CompBench. The former is for a more general image generation task, and the latter is for a more attributes- and composition-oriented image generation task.

Models. We use the newly released FLUX.1-dev model as our backbone, which is currently at the frontier of text-to-image generation and representative of the capabilities of many contemporary text-conditioned diffusion models.

Verifiers. We expand the choice of verifiers to cope with the complex nature of text-conditioned image generation: Aesthetic Score Predictor, CLIPScore, and ImageReward, to evaluate the visual quality, text-image alignment, and human preferences, respectively. Additionally, we combine these verifiers to create a Verifier Ensemble, to further expand the capacity of verifiers across the evaluative aspects. It uses the unweighted average ranking of the three verifiers as the final score.

Metrics. On DrawBench, we use all verifiers not employed in the search process as primary metrics to provide a more comprehensive evaluation. Considering the usage of Verifier Ensemble, we additionally introduce an LLM grader as a neutral evaluator for assessing sample qualities. We prompt the Gemini-1.5 model to assess synthesized images from five different perspectives: Accuracy to Prompt, Originality, Visual Quality, Internal Consistency, and Emotional Resonance. Each perspective is rated on a scale from 0 to 100, and the averaged overall score is used as the final metric.
On T2I-CompBench, we use the evaluation pipeline provided to assess the performance of our framework in compositional generation tasks.

Analysis Results: Verifier Hacking and Verifier-Task Alignment

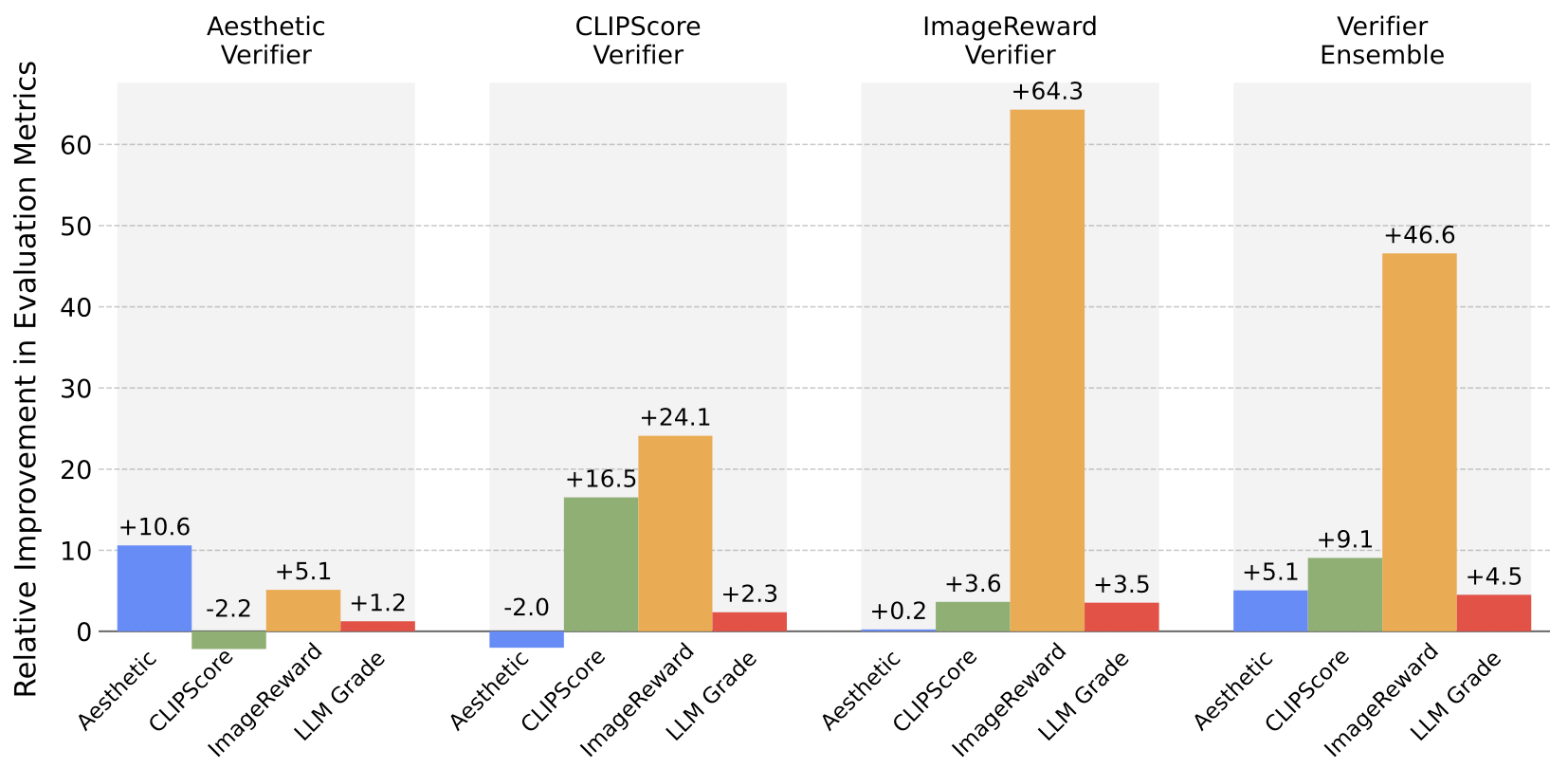
DrawBench. As shown above, and as indicated by the LLM Grader, searching with all verifiers generally improves sample quality, while specific improvement behaviors vary across different setups:

• searching with ImageReward and Verifier Ensemble consistently improve scores across all evaluation metrics.
• searching with Aesthetic and CLIP verifier improve the LLM grades but slightly degrade each other.

Yet, since searching with Aesthetic and CLIP does not lead to a total collapse in sample quality, they can be well-suited for tasks that require a focus on specific attributes such as visual appeal or textual accuracy, rather than maintaining general-purpose performance. These different behaviors across verifiers highlight the importance of aligning verifiers with the specific task at hand.

T2I-CompBench. Since T2I-CompBench emphasize correctness in relation to the text prompt, we see that ImageReward becomes the best verifier, whereas Aesthetic Score leads to minimal improvements and even degradation, as demonstrated below.

These contrasting behaviors of verifiers on DrawBench and T2I-CompBench highlight how certain verifiers can be better suited for particular tasks than others. This inspires the design of more task-specific verifiers, which we leave as future works.

Algorithms. Below we demonstrate the performance of search algorithms on DrawBench. For Zero-Order Search, we set the number of neighbors to be $N = 2$. For Search over Paths, we set the number of initial noises to be $N = 2$ as well.

We see that all three methods can effectively improve the sampling quality, with random search outperforming the other two methods in some aspects, due to the locality nature of Zero-Order Search and Search over Paths.

Search is Compatible with Finetuning

Both search and finetuning methods aim to align the final samples with explicit reward models or human preferences. While the former shifts the sample modes toward the bias of specific verifiers, the latter directly modifies the model's distribution to align with the rewards. This raises a natural question: can we still shift the sample modes according to verifiers after the model distribution has been modified?

We take the DPO fine-tuned Stable Diffusion XL model and conduct search on the DrawBench dataset. Since the model is finetuned on the dataset Pick-a-Pic, we replace ImageReward with the PickScore evaluator. The results are included below.

We see that search method can generalize to different models and can improve the performance of an already aligned model. This will be a useful tool to mitigate the cases where finetuned models disagree with reward models and to improve their generalizability.

Axes of Inference Compute Investment

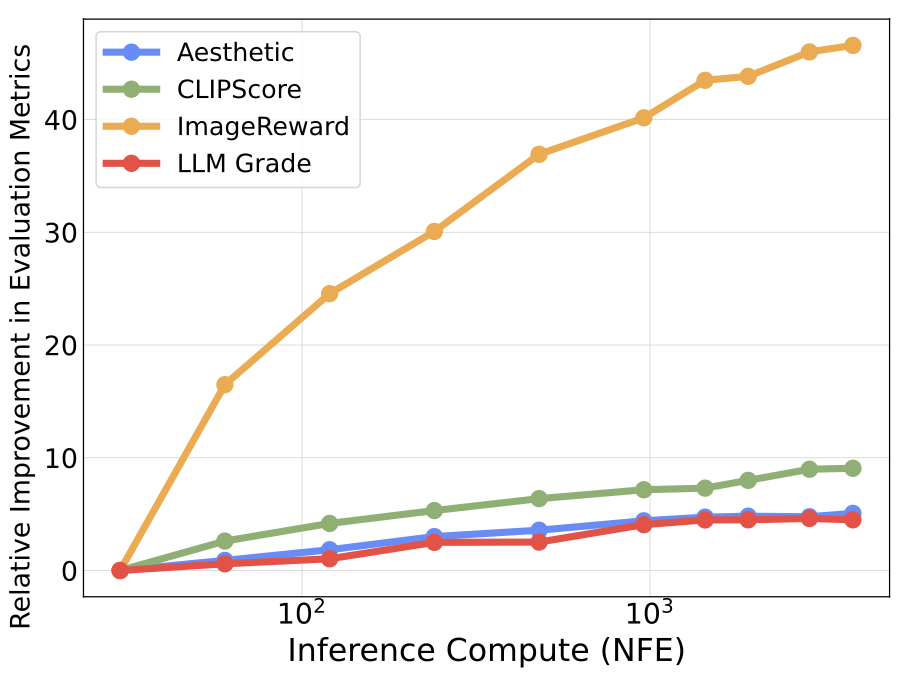
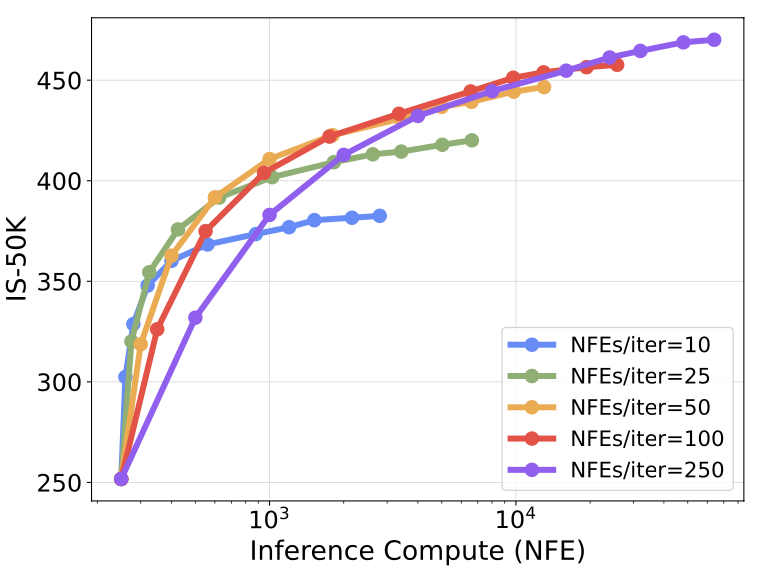
Number of search iterations. Increasing the allows the selected noises to approach the optimal set with respect to verifiers. We observed such behavior in all of our previous experiments.

Compute per search iteration. We denote such compute NFEs/iter. During search, adjusting NFEs/iter can reveal distinct compute-optimal regions, as shown below.

Effectiveness of Investing Compute

We explore the effectiveness of scaling inference-time compute for smaller diffusion models and highlight its efficiency relative to the performance of their larger counterparts without search. For ImageNet tasks, we utilize SiT-B and SiT-L, and for text-to-image tasks, we use the smaller transformer-based model PixArt-$\Sigma$ besides FLUX.1-dev.

Since models of different sizes incur significantly different costs per forward pass, we use estimated GFLOPs to measure their computational cost instead of NFEs.

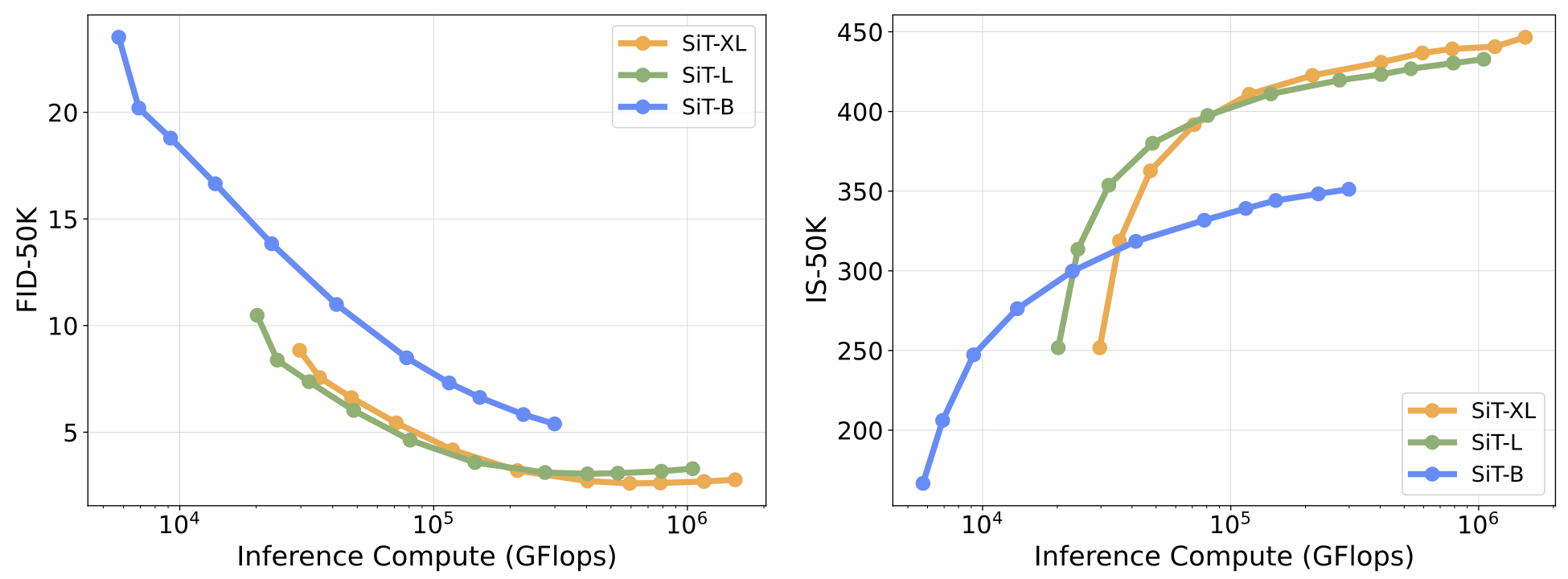
As shown above, scaling inference-time compute for small models on ImageNet can be highly effective - fixing compute budget, SiT-L can outperform SiT-XL in regions with limited inference compute. Yet, this requires the small model to have a relatively strong performance - SiT-B does not benefit from search as much as SiT-L and does not have an advantageous compute region.

These observations extend to the text-conditioned setting, as demonstrated below. With just one-tenth of the compute, PixArt-$\Sigma$ outperforms FLUX- 1.dev without search, and with roughly double the compute, PixArt-$\Sigma$ surpasses FLUX.1-dev without search by a significant margin. These results have important practical implications: the substantial compute resources invested in training can be offset by a fraction of that compute during generation, enabling access to higher-quality samples more efficiently.

Conclusion

In this work, we present a framework for inference-time scaling in diffusion models, demonstrating that scaling compute through search could significantly improve performances across various model sizes and generation tasks, and different inference-time compute budget can lead to varied scaling behavior. Identifying verifiers and algorithms as two crucial design axes in our search framework, we show that optimal configurations vary by task, with no universal solution. Additionally, our investigation into the alignment between different verifiers and generation tasks uncovers their inherent biases, highlighting the need for more carefully designed verifiers to align with specific vision generation tasks.